Một số bài tập hình học

Thứ bảy - 24/10/2020 09:59

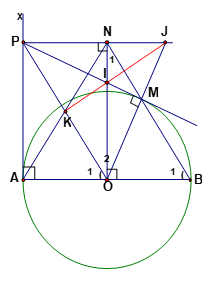
Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng:

Tứ giác CEHD, nội tiếp .
Bốn điểm B,C,E,F cùng nằm trên một đường tròn.
AE.AC = AH.AD; AD.BC = BE.AC.
H và M đối xứng nhau qua BC. Xác định tâm đường tròn nội tiếp tam giác DEF

HD GIẢI:

Xét tứ giác CEHD ta có:

Ð CEH = 90⁰( Vì BE là đường cao)
Ð CDH = 90⁰( Vì AD là đường cao)
=> Ð CEH + Ð CDH = 180⁰
Mà Ð CEH và Ð CDH là hai góc đối của tứ giác CEHD , Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ^ AC => ÐBEA = 90⁰.
AD là đường cao => AD ^ BC => ÐBDA = 90⁰.
Như vậy E và D cùng nhìn AB dưới một góc 90⁰ => E và D cùng nằm trên đường tròn đường kính AB.
Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.
3. Theo giả thiết tam giác ABC cân tại A có AD là đường cao nên cũng là đường trung tuyến

HD GIẢI:

Theo tính chất hai tiếp tuyến cắt nhau ta có: CA = CM; DB = DM => AC + BD = CM + DM.

Mà CM + DM = CD => AC + BD = CD

Theo tính chất hai tiếp tuyến cắt nhau ta có: OC là tia phân giác của góc AOM; OD là tia phân giác của góc BOM, mà ÐAOM và ÐBOM là hai góc kề bù => ÐCOD = 90⁰.
Theo trên ÐCOD = 90⁰ nên tam giác COD vuông tại O có OM ^ CD ( OM là tiếp tuyến ).

áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có OM² = CM. DM,

Theo trên ÐCOD = 90⁰ nên OC ^ OD .(1)

Theo tính chất hai tiếp tuyến cắt nhau ta có: DB = DM; lại có OM = OB =R => OD là trung trực của BM => BM ^ OD .(2). Từ (1) Và (2) => OC // BM ( Vì cùng vuông góc với OD).

Gọi I là trung điểm của CD ta có I là tâm đường tròn ngoại tiếp tam giác COD đường kính CD có IO là bán kính.

Theo tính chất tiếp tuyến ta có AC ^ AB; BD ^ AB => AC // BD => tứ giác ACDB là hình thang. Lại có I là trung điểm của CD; O là trung điểm của AB => IO là đường trung bình của hình thang ACDB
=> IO // AC , mà AC ^ AB => IO ^ AB tại O => AB là tiếp tuyến tại O của đường tròn đường kính CD

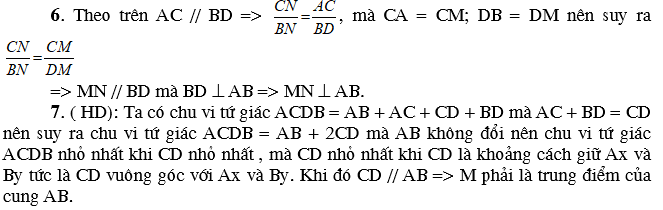
HD GIẢI:
1. Vì I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp góc A nên BI và BK là hai tia phân giác của hai góc kề bù đỉnh B
Do đó BI ^ BK hayÐIBK = 90⁰ .
Tương tự ta cũng có ÐICK = 90⁰ như vậy B và C cùng nằm trên đường tròn đường kính IK do đó B, C, I, K cùng nằm trên một đường tròn.

Ta có ÐC₁ = ÐC₂ (1) ( vì CI là phân giác của góc ACH.

ÐC₂ + ÐI₁ = 90⁰ (2) ( vì ÐIHC = 90⁰ ).
ÐI₁ = Ð ICO (3) ( vì tam giác OIC cân tại O)

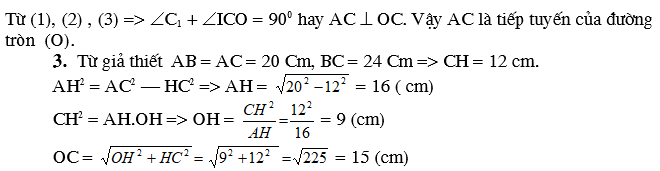
Bài 5 Cho đường tròn (O; R), từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kì ( M khác A) kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ AC ^ MB, BD ^ MA, gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB.

Chứng minh tứ giác AMBO nội tiếp.
Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn .
Chứng minh OI.OM = R²; OI. IM = IA².
Chứng minh OAHB là hình thoi.
Chứng minh ba điểm O, H, M thẳng hàng.
Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳng d

HD GIẢI:

(HS tự làm).

Vì K là trung điểm NP nên OK ^ NP ( quan hệ đường kính

Và dây cung) => ÐOKM = 90⁰. Theo tính chất tiếp tuyến ta có ÐOAM = 90⁰; ÐOBM = 90⁰. như vậy K, A, B cùng nhìn OM dưới một góc 90⁰ nên cùng nằm trên đường tròn đường kính OM.
Vậy năm điểm O, K, A, M, B cùng nằm trên một đường tròn.
3. Ta có MA = MB ( t/c hai tiếp tuyến cắt nhau); OA = OB = R
=> OM là trung trực của AB => OM ^ AB tại I .
Theo tính chất tiếp tuyến ta có ÐOAM = 90⁰ nên tam giác OAM vuông tại A có AI là đường cao.
áp dụng hệ thức giữa cạnh và đường cao => OI.OM = OA² hay OI.OM = R²; và OI. IM = IA².
4. Ta có OB ^ MB (tính chất tiếp tuyến) ; AC ^ MB (gt) => OB // AC hay OB // AH.
OA ^ MA (tính chất tiếp tuyến) ; BD ^ MA (gt) => OA // BD hay OA // BH.
=> Tø gi¸c OAHB lµ h×nh b×nh hµnh; l¹i cã OA = OB (=R) => OAHB lµ h×nh thoi.
5. Theo trªn OAHB lµ h×nh thoi. => OH ^ AB; còng theo trªn OM ^ AB => O, H, M th¼ng hµng( V× qua O chØ cã mét ®êng th¼ng vu«ng gãc víi AB).
6. (HD) Theo trªn OAHB lµ h×nh thoi. => AH = AO = R. VËy khi M di ®éng trªn d th× H còng di ®éng nhng lu«n c¸ch A cè ®Þnh mét kho¶ng b»ng R. Do ®ã quü tÝch cña ®iÓm H khi M di chuyÓn trªn ®êng th¼ng d lµ nöa ®êng trßn t©m A b¸n kÝnh AH = R
Bài 6 Cho tam giác ABC vuông ở A, đường cao AH. Vẽ đường tròn tâm A bán kính AH. Gọi HD là đường kính của đường tròn (A; AH). Tiếp tuyến của đường tròn tại D cắt CA ở E.

Chứng minh tam giác BEC cân.

Gọi I là hình chiếu của A trên BE, Chứng minh rằng AI = AH.
Chứng minh rằng BE là tiếp tuyến của đường tròn (A; AH).
Chứng minh BE = BH + DE.

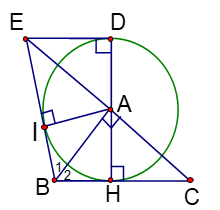
HD GIẢI:

D AHC = DADE (g.c.g) => ED = HC (1) và AE = AC (2).

Vì AB ^CE (gt), do đó AB vừa là đường cao vừa là đường trung tuyến của DBEC => BEC là tam giác cân. => ÐB₁ = ÐB₂
2. Hai tam giác vuông ABI và ABH có cạnh huyền AB chung, ÐB₁ = ÐB₂ => D AHB = DAIB
=> AI = AH.
3. AI = AH và BE ^ AI tại I => BE là tiếp tuyến của (A; AH) tại I.
4. DE = IE và BI = BH => BE = BI+IE = BH + ED
Bài 7 Cho đường tròn (O; R) đường kính AB. Kẻ tiếp tuyến Ax và lấy trên tiếp tuyến đó một điểm P sao cho AP > R, từ P kẻ tiếp tuyến tiếp xúc với (O) tại M.

Chứng minh rằng tứ giác APMO nội tiếp được một đường tròn.
Chứng minh BM // OP.
Đường thẳng vuông góc với AB ở O cắt tia BM tại N. Chứng minh tứ giác OBNP là hình bình hành.

Biết AN cắt OP tại K, PM cắt ON tại I; PN và OM kéo dài cắt nhau tại J. Chứng minh I, J, K thẳng hàng.

AONP là hình chữ nhật => ÐAPO = Ð NOP ( so le) (7)
Theo t/c hai tiếp tuyến cắt nhau Ta có PO là tia phân giác ÐAPM => ÐAPO = ÐMPO (8).
Từ (7) và (8) => DIPO cân tại I có IK là trung tuyến đông thời là đường cao => IK ^ PO. (9)
Từ (6) và (9) => I, J, K thẳng hàng.
Bài 8 Cho nửa đường tròn tâm O đường kính AB và điểm M bất kì trên nửa đường tròn ( M khác A,B). Trên nửa mặt phẳng bờ AB chứa nửa đường tròn kẻ tiếp tuyến Ax. Tia BM cắt Ax tại I; tia phân giác của góc IAM cắt nửa đường tròn tại E; cắt tia BM tại F tia BE cắt Ax tại H, cắt AM tại K.
1) Chứng minh rằng: EFMK là tứ giác nội tiếp.
2) Chứng minh rằng: AI² = IM . IB.
3) Chứng minh BAF là tam giác cân.
4) Chứng minh rằng : Tứ giác AKFH là hình thoi.
5) Xác định vị trí M để tứ giác AKFI nội tiếp được một đường tròn.

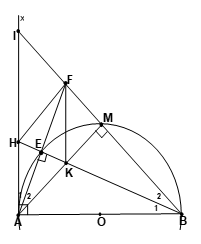
HD GIẢI:
1. Ta có : ÐAMB = 90⁰ ( nội tiếp chắn nửa đường tròn )
=> ÐKMF = 90⁰ (vì là hai góc kề bù).
ÐAEB = 90⁰ ( nội tiếp chắn nửa đường tròn )
=> ÐKEF = 90⁰ (vì là hai góc kề bù).
=> ÐKMF + ÐKEF = 180⁰ . Mà ÐKMF và ÐKEF là hai góc đối của tứ giác EFMK do đó EFMK là tứ giác nội tiếp.

Ta có ÐIAB = 90⁰ ( vì AI là tiếp tuyến ) => DAIB vuông tại A có AM ^ IB ( theo trên).

áp dụng hệ thức giữa cạnh và đường cao => AI² = IM . IB.

Theo giả thiết AE là tia phân giác góc IAM => ÐIAE = ÐMAE => AE = ME

=> ÐABE =ÐMBE ( hai góc nội tiếp chắn hai cung bằng nhau) => BE là tia phân giác góc ABF. (1)
Theo trên ta có ÐAEB = 90⁰ => BE ^ AF hay BE là đường cao của tam giác ABF (2).
Từ (1) và (2) => BAF là tam giác cân. tại B .

BAF là tam giác cân. tại B có BE là đường cao nên đồng thời là đương trung tuyến => E là trung điểm của AF. (3)

Từ BE ^ AF => AF ^ HK (4), theo trên AE là tia phân giác góc IAM hay AE là tia phân giác ÐHAK (5)
Từ (4) và (5) => HAK là tam giác cân. tại A có AE là đường cao nên đồng thời là đương trung tuyến => E là trung điểm của HK. (6).
Từ (3) , (4) và (6) => AKFH là hình thoi ( vì có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường).