ĐỀ CƯƠNG ÔN TẬP HỌC KỲ I TOÁN 9
1) Trả lời 5 câu hỏi ôn tập chương I và thuộc 9 công thức biến đổi căn thức SGK trang 19
2) Học thuộc phần tóm tắt các kiến thức cần nhớ chương II SGK trang 60
• Hình học :
1) Học thuộc phần tóm tắt các kiến thức cần nhớ chương I SGK trang 92
2) Học thuộc phần tóm tắt các kiến thức cần nhớ chương II SGK trang 60
2) Học thuộc phần tóm tắt các kiến thức cần nhớ chương II SGK trang 60
• Hình học :
1) Học thuộc phần tóm tắt các kiến thức cần nhớ chương I SGK trang 92
2) Học thuộc phần tóm tắt các kiến thức cần nhớ chương II SGK trang 60



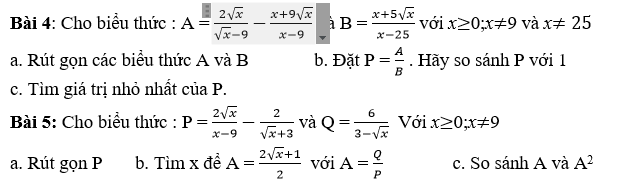
Bài 6: Cho đường thẳng d : y=(3 – 2m)x – 2m – 5 (m là tham số)
a. Với giá trị nào của m thì đường thẳng d cắt trục tung tại điểm có tung độ bằng -3
b. Tìm m để đường thẳng d song song với đường thẳng y = 2015 – x
c. Tìm điểm cố định mà đường thẳng d luôn luôn đi qua với mọi m
d. Tìm phương trình đường thẳng d biết đồ thị đi qua I(2:2) và có hệ số góc bằng -2
Bài 7 : Cho hàm số bậc nhất y=(1-2m)x - 1 có đồ thị là (d)
a. Tìm m để đồ thị hàm số trên song song với đồ thị hàm số y= 2x + 3
b. Vẽ đồ thị hàm số với m vừa tìm được ở câu a.
c. Tìm m để (d) và đường thẳng y=-3x + 1 cắt nhau tại một điểm có hoành độ bằng 1
d*. Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng (d) là lớn nhất
Bài 8 : Cho các đường thẳng (d1) : y = 4mx - (m+5) với m0; (d2) : y = (3m + 1)x + (m - 9)
a. Với giá trị nào của m thì (d1)//(d2)
b. Với giá trị nào của m thì (d1) cắt (d2). Tìm tọa độ giao điểm khi m=2
c. Chứng minh rằng khi m thay đổi thì đường thẳng (d) luôn đi qua điểm cố định A; (d2) đi qua điểm cố định B
Bài 9: Cho hàm số y = ax + b
a. Xác định hàm số biết đồ thị hàm số song song với y = 2x + 3
b. Vẽ đồ thị hàm số vừa xác định rồi tính độ lớn góc α
c. Tìm toạ độ giao điểm của đường thẳng trên với đường thẳng y = -4x + 3
d. Tìm giá trị của m để đường thẳng trên song song với đường thẳng y = (2m - 3)x + 2
Bài 10 : Cho hàm số y = (m - 1)x + 2 (m ≠
a. Tìm điều kiện của m để hàm số (1) đồng biến trên R
b. Tìm m biết đồ thị hàm số (1) là đường thẳng có hệ số góc bằng 2
c. Tìm m biết đồ thị hàm số (1) đi qua điểm A(2;-1)
d. Tìm m biết đồ thị hàm số(1)cắt hai trục toạ độ tạo thành tam giác có diện tích bằng 4
Bài 11: Cho hàm số bậc nhất y = (m-2)x + 2m - 5 có đồ thị là đường thẳng d
- Tìm m để d cắt trục tung tại điểm có tung độ bằng 3
- Vẽ đồ thị với m tìm được ở câu a
- Tìm m biết đường thẳng d vuông góc với d1 : 2x - y + 3 = 0
- Chứng tỏ rằng đương thẳng d luôn đi qua một điểm cố định.
- Tìm m để khoảng cách từ M(2;0) đến d là lớn nhất
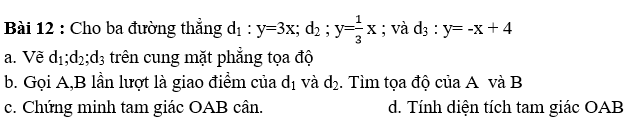

Bài 15 : Cho đường tròn (O;5cm), đường kính AB. Gọi E là một điểm trên AB sao cho BE= 2cm. Qua trung điểm H của AE vẽ dây cung CD ⊥AB
- Tứ giác ACED là hình gì ? Vì sao ?
- Gọi I là giao điểm của DE với BC.Chứng minh I thuộc đường tròn (O’) đường kính EB
- Chứng minh HI là tiếp tuyến của đường tròn (O’)
- Tính độ dài đoạn HI
- Chứng minh AMN vuông
- △
 IOO’ là tam giác gì? Vì sao?
IOO’ là tam giác gì? Vì sao? - Chứng minh rằng đường thẳng MN tiếp xúc với đường tròn đường kính OO’
- Cho biết OA=8cm, OA’= 4,5cm. Tính độ dài MN
- Tứ giác CEHF là hình chữ nhật
- EF là tiếp tuyến chung của các đường tròn đường kính AH và đường kính BH
- Tiếp tuyến tại A cắt đường thẳng BC tại M, gọi I là tâm hình chữ nhật CEHF, BI cắt AM ở N. Chứng mình rằng : N là trung điểm của AM.
- Chứng minh AO vuông góc với BC
- Kẻ đường kính BD. Chứng minh rằng : DC//OA
- Tính chu vi tam giác ABC
- Qua O kẻ đường thẳng vuông góc với BD,đường thẳng này cắt tia DC tại E. Đường thẳng AE và OC cắt nhau ở I, đường thẳng OE và AC cắt nhau tại G. Chứng minh IG là trung trực của đoạn thẳng OA.
- Chứng minh rằng OD là tia phân giác của BOC
- Chứng minh CD là tiếp tuyến của đường tròn.
- Qua D kẻ cát tuyến DMN với đường tròn (N nằm giữa D và M). Chứng minh : DB2=DM.DN
- Dây CM cắt đường kính AB tại I. Chứng minh rằng IC.IM=IA.IB
- Chứng minh CD = AC + BD và COD=900
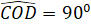
- AD cắt BC tại N. Chứng minh MN//BD
- Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn
- Gọi H là trung điểm của AM. Chứng minh O,H,C thẳng hàng
- TÍnh MH,HA,HB theo R thi góc ABM = 300
- Tứ giác <POQ là hình gì ? Vì sao ?
- Xác định vị trí của M trên nửa đường tròn (O) để diện tích tam giác EOF nhỏ nhất. Tính giá trị nhỏ nhát của R.
- CMR : P,K,Q thẳng hàng
- Chứng minh OM = OP và tam giác NMP cân.
- Hạ OI vuông góc với MN. Chứng minh OI = R và MN là tiếp tuyến của đường tròn (O)
- Chứng minh AM.BN = R2
- Tìm vị trí của M để diện tích tứ giác AMBN là nhỏ nhất
- Chứng minh : AE + BF = EF
- Chứng minh tam giác OEF là tam giác vuông
- Đường thẳng BC cắt tia Ax ở D, chứng minh E là trung điểm của AD.
- Gọi M là giao điểm của OE và AC, N là giao điểm của OF và BC, H là hình chiếu của C trên AB. Chứng tỏ khi C di động trên đường tròn tâm O thì đường tròn ngoại tiếp tam giác MHN luôn đi qua một điểm cố định.
Ý kiến bạn đọc
Bạn cần đăng nhập với tư cách là Thành viên chính thức để có thể bình luận
Những tin mới hơn
Những tin cũ hơn
global video
-
-
 Hướng dẫn giải bài tập về vận...
hướng dẫn ôn tập và giải các bài tập về
Hướng dẫn giải bài tập về vận...
hướng dẫn ôn tập và giải các bài tập về
-
 Hướng dẫn giải bài tập về công...
hướng dẫn ôn tập và giải các bài tập về công cơ học
Hướng dẫn giải bài tập về công...
hướng dẫn ôn tập và giải các bài tập về công cơ học
-
 Hướng dẫn giải bài tập về lực...
Hướng dẫn giải bài tập về
Hướng dẫn giải bài tập về lực...
Hướng dẫn giải bài tập về
Thăm dò ý kiến
Tin xem nhiều
-
 Bài tập về thấu kính hội tụ
Bài tập về thấu kính hội tụ
-
 DẠNG TOÁN HỖN HỢP TRONG HÓA HỌC
DẠNG TOÁN HỖN HỢP TRONG HÓA HỌC
-
 ĐỀ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 MÔN GDCD
ĐỀ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 MÔN GDCD
-
 ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 MÔN NGỮ VĂN
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 MÔN NGỮ VĂN
-
 Bài tập về thấu kính phân kỳ
Bài tập về thấu kính phân kỳ
-
 Dạng bài tập về Đoạn mạch nối tiếp
Dạng bài tập về Đoạn mạch nối tiếp
-
 Cách mạng tháng tám 1945: Thời cơ, diễn biến, ý nghĩa lịch sử và bài học kinh nghiệm của cách mạng tháng tám 1945
Cách mạng tháng tám 1945: Thời cơ, diễn biến, ý nghĩa lịch sử và bài học kinh nghiệm của cách mạng tháng tám 1945
-
 Dạng bài tập đoạn mạch song song
Dạng bài tập đoạn mạch song song
-
 CUỘC CÁCH MẠNG KHOA HỌC KĨ THUẬT LẦN THỨ HAI
CUỘC CÁCH MẠNG KHOA HỌC KĨ THUẬT LẦN THỨ HAI
-
 TRỢ TỪ – THÁN TỪ – TÌNH THÁI TỪ
TRỢ TỪ – THÁN TỪ – TÌNH THÁI TỪ
Thống kê
- Đang truy cập85
- Hôm nay22,437
- Tháng hiện tại742,351
- Tổng lượt truy cập18,830,535
Tài liệu mới
- chuyên đề Phương trình... - 18/04/2022
- Phương trình chứa ấn ở... - 28/02/2020
- Các dạng bài tập phương... - 28/02/2020
- Giáo án dạy thêm toán 6 - 27/02/2020
- Chuyên đề bồi dưỡng học... - 27/02/2020
