Một só bài tập chuyển động cơ học hay
Bài 1: Trên một đường gấp khúc tại thành một tam giác đều ABC cạnh a = 30m, có hai xe khởi hành cùng lúc tại A. Xe (I) chuyển động theo hướng AB với vận tốc không đổi v1 = 3m/s; Xe (II) chuyển động theo hướng AC, với vận tốc không đổi v2 = 2m/s. Mỗi xe chạy 5 vòng.
Hãy xác định số lần hai xe gặp nhau, vị trí vả thời điểm hai xe gặp nhau (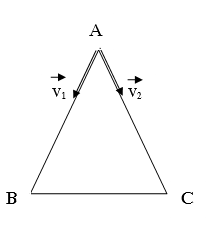 không kể những lần hai xe gặp nhau ở A).
không kể những lần hai xe gặp nhau ở A).
Giải
Ta có chu vi của đường ABC là: s = 3a = 3.30 = 90 (m).
Hai xe gặp nhau khi tổng quãng đường đi từ đầu (hay lần gặp nhau trước đó) đúng bằng chu vi của tam giác.
Vậy khoảng thời gian giữa hai lần gặp nhau liên tiếp được tính bởi:
v1t + v2t = S
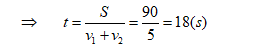
Vậy chọn gốc thời gian là lúc khởi hành thì các thời điểm gặp nhau là:
t1 = 1.18(s)
t2 = 2.18 = 36(s)
t3 = 3.18 = 54(s)
..................................
tn = n.18 = 18n(s).
Ngoài ra v1 > v2 nên với 5 vòng chạy thì xe (I) đi hết thời gian:
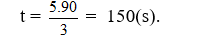
Xe (I) tới A vào những thời điểm:
t'1 = 30s; t'2 = 60s; t'1 = 30s; t'3 = 90s; t'4 = 120s; t'5 = 150s.
Ta suy ra:
- Không kể những lần gặp nhau ở A thì hai xe gặp nhau trên đường đi ở các thời điểm:
t1 = 18s; t2 = 36s; t3 = 54s; t4 = 72s; t6 = 108s; t7 = 126s; t8 = 144s.
Có tất cả 7 lần gặp nhau trên đường đi.
- Vị trí gặp nhau được tính từ các thời điển trên và so với đỉnh gần nhất là:
 Lần 1: Cách C đoạn CM1 = 6m theo chiều CB
Lần 1: Cách C đoạn CM1 = 6m theo chiều CB
 Lần 2: Cách B đoạn BM2 = 12m theo chiều BA
Lần 2: Cách B đoạn BM2 = 12m theo chiều BA
 Lần 2: Cách C đoạn CM3 = 6m theo chiều CA
Lần 2: Cách C đoạn CM3 = 6m theo chiều CA
 Lần 4: Cách B đoạn BM4 = 6m theo chiều BC
Lần 4: Cách B đoạn BM4 = 6m theo chiều BC
 Lần 5: Cách C đoạn CM5 = 6m theo chiều CB
Lần 5: Cách C đoạn CM5 = 6m theo chiều CB
(bỏ lần gặp ở A và do đó coi như hai xe lại chuyển động bắt đầu từ A).
 Lần 6: Cách B đoạn BM6 = 12m theo chiều BA
Lần 6: Cách B đoạn BM6 = 12m theo chiều BA
 Lần 7: Cách C đoạn CM7 = 12m theo chiều CA.
Lần 7: Cách C đoạn CM7 = 12m theo chiều CA.
Xe (I) tới A vào những thời điểm:
t'1 = 30s; t'2 = 60s; t'1 = 30s; t'3 = 90s; t'4 = 120s; t'5 = 150s.
Ta suy ra:
- Không kể những lần gặp nhau ở A thì hai xe gặp nhau trên đường đi ở các thời điểm:
t1 = 18s; t2 = 36s; t3 = 54s; t4 = 72s; t6 = 108s; t7 = 126s; t8 = 144s.
Có tất cả 7 lần gặp nhau trên đường đi.
- Vị trí gặp nhau được tính từ các thời điển trên và so với đỉnh gần nhất là:
 Lần 1: Cách C đoạn CM1 = 6m theo chiều CB
Lần 1: Cách C đoạn CM1 = 6m theo chiều CB
 Lần 2: Cách B đoạn BM2 = 12m theo chiều BA
Lần 2: Cách B đoạn BM2 = 12m theo chiều BA
 Lần 2: Cách C đoạn CM3 = 6m theo chiều CA
Lần 2: Cách C đoạn CM3 = 6m theo chiều CA
 Lần 4: Cách B đoạn BM4 = 6m theo chiều BC
Lần 4: Cách B đoạn BM4 = 6m theo chiều BC
 Lần 5: Cách C đoạn CM5 = 6m theo chiều CB
Lần 5: Cách C đoạn CM5 = 6m theo chiều CB
(bỏ lần gặp ở A và do đó coi như hai xe lại chuyển động bắt đầu từ A).
 Lần 6: Cách B đoạn BM6 = 12m theo chiều BA
Lần 6: Cách B đoạn BM6 = 12m theo chiều BA
 Lần 7: Cách C đoạn CM7 = 12m theo chiều CA.
Lần 7: Cách C đoạn CM7 = 12m theo chiều CA.
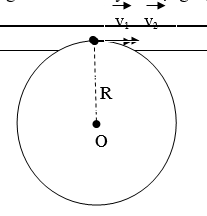 Giải
Giải



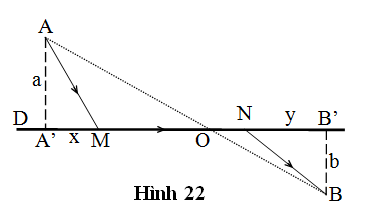
Bài 3: Một ôtô xuất phát từ điểm A trên cánh đồng để đến điểm B trên sân vận động (Hình 22). Cánh đồng và sân vận động được ngăn cách nhau bởi con đường thẳng D, khoảng cách từ A đến đường D là a=400m, khoảng cách từ B đến đường D là b=300m, khoảng cách AB=2,8km. Biết tốc độ của ôtô trên cánh đồng là v=3km/h, trên đường D là 5v/3, trên sân vận động là 4v/3. Hỏi ôtô phải đi đến điểm M trên đường cách A’ một khoảng x và rời đường tại N cách B’ một khoảng y bằng bao nhiêu để thời gian chuyển động là nhỏ nhất? Xác định khoảng thời gian nhỏ nhất đó?

Giải

Bài 4: Từ một điểm A trên con sông thẳng, cùng lúc có một cái phao trôi theo dòng nước và một con cá bơi xuôi dòng đến một cái cầu C cách A 3,75km rồi ngay lập tức cá bơi ngược trở lại gặp phao tại một điểm B cách A 1,5km hết thời gian là 0,5 giờ. Biết rằng nước chảy ổn định và vận tốc của cá so với dòng nước là không đổi.
a. Tìm vận tốc của dòng nước và vận tốc của cá so với dòng nước.
b. Giả sử sau khi gặp phao con cá bơi quay lại đến cầu C rồi lại bơi ngược dòng tới gặp phao, lại bơi quay lại cầu C, cứ thế bơi qua lại giữa phao và cầu C... cuối cùng dừng lại cùng phao tại cầu C. Tìm độ dài quãng đường mà cá đã bơi được.

Bài 5: Một ca nô xuất phát từ bến sông A có vận tốc đối với nước là 12km/h, chạy thẳng xuôi dòng đuổi theo 1 xuồng máy đang có vận tốc đối với bờ là 10km/h khởi hành trước đó 2h từ bến B trên cùng dòng sông. Khi chạy ngang qua B, ca nô thay đổi vận tốc để có vận tốc đối với bờ tăng lên gấp đôi và sau đó 3h đã đuổi kịp xuồng máy. Biết khoảng cách AB là 60km. Tính vận tốc của dòng nước.
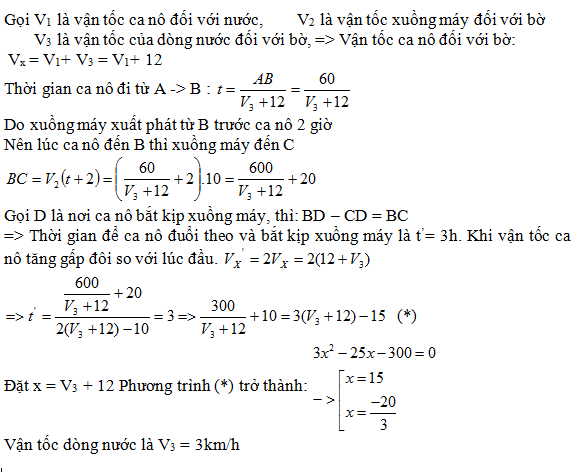
 không kể những lần hai xe gặp nhau ở A).
không kể những lần hai xe gặp nhau ở A).Giải
Ta có chu vi của đường ABC là: s = 3a = 3.30 = 90 (m).
Hai xe gặp nhau khi tổng quãng đường đi từ đầu (hay lần gặp nhau trước đó) đúng bằng chu vi của tam giác.
Vậy khoảng thời gian giữa hai lần gặp nhau liên tiếp được tính bởi:
v1t + v2t = S
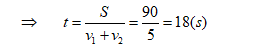
Vậy chọn gốc thời gian là lúc khởi hành thì các thời điểm gặp nhau là:
t1 = 1.18(s)
t2 = 2.18 = 36(s)
t3 = 3.18 = 54(s)
..................................
tn = n.18 = 18n(s).
Ngoài ra v1 > v2 nên với 5 vòng chạy thì xe (I) đi hết thời gian:
Xe (I) tới A vào những thời điểm:
t'1 = 30s; t'2 = 60s; t'1 = 30s; t'3 = 90s; t'4 = 120s; t'5 = 150s.
Ta suy ra:
- Không kể những lần gặp nhau ở A thì hai xe gặp nhau trên đường đi ở các thời điểm:
t1 = 18s; t2 = 36s; t3 = 54s; t4 = 72s; t6 = 108s; t7 = 126s; t8 = 144s.
Có tất cả 7 lần gặp nhau trên đường đi.
- Vị trí gặp nhau được tính từ các thời điển trên và so với đỉnh gần nhất là:
 Lần 1: Cách C đoạn CM1 = 6m theo chiều CB
Lần 1: Cách C đoạn CM1 = 6m theo chiều CB Lần 2: Cách B đoạn BM2 = 12m theo chiều BA
Lần 2: Cách B đoạn BM2 = 12m theo chiều BA Lần 2: Cách C đoạn CM3 = 6m theo chiều CA
Lần 2: Cách C đoạn CM3 = 6m theo chiều CA Lần 4: Cách B đoạn BM4 = 6m theo chiều BC
Lần 4: Cách B đoạn BM4 = 6m theo chiều BC  Lần 5: Cách C đoạn CM5 = 6m theo chiều CB
Lần 5: Cách C đoạn CM5 = 6m theo chiều CB (bỏ lần gặp ở A và do đó coi như hai xe lại chuyển động bắt đầu từ A).
 Lần 6: Cách B đoạn BM6 = 12m theo chiều BA
Lần 6: Cách B đoạn BM6 = 12m theo chiều BA Lần 7: Cách C đoạn CM7 = 12m theo chiều CA.
Lần 7: Cách C đoạn CM7 = 12m theo chiều CA.Xe (I) tới A vào những thời điểm:
t'1 = 30s; t'2 = 60s; t'1 = 30s; t'3 = 90s; t'4 = 120s; t'5 = 150s.
Ta suy ra:
- Không kể những lần gặp nhau ở A thì hai xe gặp nhau trên đường đi ở các thời điểm:
t1 = 18s; t2 = 36s; t3 = 54s; t4 = 72s; t6 = 108s; t7 = 126s; t8 = 144s.
Có tất cả 7 lần gặp nhau trên đường đi.
- Vị trí gặp nhau được tính từ các thời điển trên và so với đỉnh gần nhất là:
 Lần 1: Cách C đoạn CM1 = 6m theo chiều CB
Lần 1: Cách C đoạn CM1 = 6m theo chiều CB Lần 2: Cách B đoạn BM2 = 12m theo chiều BA
Lần 2: Cách B đoạn BM2 = 12m theo chiều BA Lần 2: Cách C đoạn CM3 = 6m theo chiều CA
Lần 2: Cách C đoạn CM3 = 6m theo chiều CA Lần 4: Cách B đoạn BM4 = 6m theo chiều BC
Lần 4: Cách B đoạn BM4 = 6m theo chiều BC  Lần 5: Cách C đoạn CM5 = 6m theo chiều CB
Lần 5: Cách C đoạn CM5 = 6m theo chiều CB (bỏ lần gặp ở A và do đó coi như hai xe lại chuyển động bắt đầu từ A).
 Lần 6: Cách B đoạn BM6 = 12m theo chiều BA
Lần 6: Cách B đoạn BM6 = 12m theo chiều BA Lần 7: Cách C đoạn CM7 = 12m theo chiều CA.
Lần 7: Cách C đoạn CM7 = 12m theo chiều CA.
Bài 2: Hai xe (I) và (II) chuyển động trên một đường tròn với vận tốc không đổi. Xe (I) đi hết 1 vòng mất 10phút, xe (II) đi 1 vòng 50phút.
Hỏi khi xe (II) đi 1 vòng thì gặp xe (I) mấy lần, trong các trường hợp sau đây?
a. Hai xe khởi hành cùng lúc tại một điểm trên đường tròn và chuyển động cùng chiều.
b. Hai xe khởi hành cùng lúc tại một điểm trên đường tròn và chuyển động ngược chiều.
Hỏi khi xe (II) đi 1 vòng thì gặp xe (I) mấy lần, trong các trường hợp sau đây?
a. Hai xe khởi hành cùng lúc tại một điểm trên đường tròn và chuyển động cùng chiều.
b. Hai xe khởi hành cùng lúc tại một điểm trên đường tròn và chuyển động ngược chiều.
 Giải
Giải


Bài 3: Một ôtô xuất phát từ điểm A trên cánh đồng để đến điểm B trên sân vận động (Hình 22). Cánh đồng và sân vận động được ngăn cách nhau bởi con đường thẳng D, khoảng cách từ A đến đường D là a=400m, khoảng cách từ B đến đường D là b=300m, khoảng cách AB=2,8km. Biết tốc độ của ôtô trên cánh đồng là v=3km/h, trên đường D là 5v/3, trên sân vận động là 4v/3. Hỏi ôtô phải đi đến điểm M trên đường cách A’ một khoảng x và rời đường tại N cách B’ một khoảng y bằng bao nhiêu để thời gian chuyển động là nhỏ nhất? Xác định khoảng thời gian nhỏ nhất đó?

Giải

Bài 4: Từ một điểm A trên con sông thẳng, cùng lúc có một cái phao trôi theo dòng nước và một con cá bơi xuôi dòng đến một cái cầu C cách A 3,75km rồi ngay lập tức cá bơi ngược trở lại gặp phao tại một điểm B cách A 1,5km hết thời gian là 0,5 giờ. Biết rằng nước chảy ổn định và vận tốc của cá so với dòng nước là không đổi.
a. Tìm vận tốc của dòng nước và vận tốc của cá so với dòng nước.
b. Giả sử sau khi gặp phao con cá bơi quay lại đến cầu C rồi lại bơi ngược dòng tới gặp phao, lại bơi quay lại cầu C, cứ thế bơi qua lại giữa phao và cầu C... cuối cùng dừng lại cùng phao tại cầu C. Tìm độ dài quãng đường mà cá đã bơi được.

Bài 5: Một ca nô xuất phát từ bến sông A có vận tốc đối với nước là 12km/h, chạy thẳng xuôi dòng đuổi theo 1 xuồng máy đang có vận tốc đối với bờ là 10km/h khởi hành trước đó 2h từ bến B trên cùng dòng sông. Khi chạy ngang qua B, ca nô thay đổi vận tốc để có vận tốc đối với bờ tăng lên gấp đôi và sau đó 3h đã đuổi kịp xuồng máy. Biết khoảng cách AB là 60km. Tính vận tốc của dòng nước.
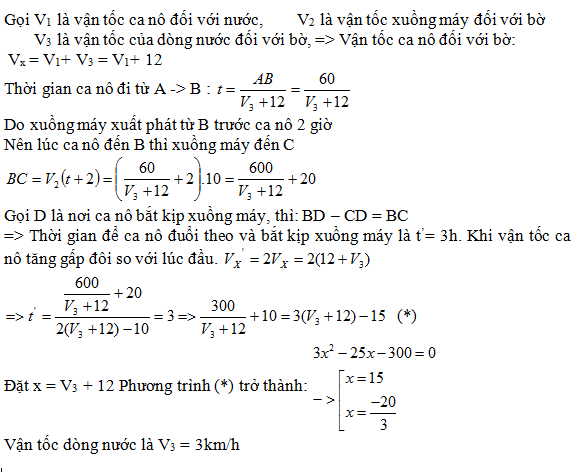
Ý kiến bạn đọc
Bạn cần đăng nhập với tư cách là Thành viên chính thức để có thể bình luận
Những tin mới hơn
Những tin cũ hơn
global video
-
-
 Hướng dẫn giải bài tập về vận...
hướng dẫn ôn tập và giải các bài tập về
Hướng dẫn giải bài tập về vận...
hướng dẫn ôn tập và giải các bài tập về
-
 Hướng dẫn giải bài tập về công...
hướng dẫn ôn tập và giải các bài tập về công cơ học
Hướng dẫn giải bài tập về công...
hướng dẫn ôn tập và giải các bài tập về công cơ học
-
 Hướng dẫn giải bài tập về lực...
Hướng dẫn giải bài tập về
Hướng dẫn giải bài tập về lực...
Hướng dẫn giải bài tập về
Thăm dò ý kiến
Tin xem nhiều
-
 Bài tập về thấu kính hội tụ
Bài tập về thấu kính hội tụ
-
 DẠNG TOÁN HỖN HỢP TRONG HÓA HỌC
DẠNG TOÁN HỖN HỢP TRONG HÓA HỌC
-
 ĐỀ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 MÔN GDCD
ĐỀ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 MÔN GDCD
-
 ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 MÔN NGỮ VĂN
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 MÔN NGỮ VĂN
-
 Bài tập về thấu kính phân kỳ
Bài tập về thấu kính phân kỳ
-
 Dạng bài tập về Đoạn mạch nối tiếp
Dạng bài tập về Đoạn mạch nối tiếp
-
 Cách mạng tháng tám 1945: Thời cơ, diễn biến, ý nghĩa lịch sử và bài học kinh nghiệm của cách mạng tháng tám 1945
Cách mạng tháng tám 1945: Thời cơ, diễn biến, ý nghĩa lịch sử và bài học kinh nghiệm của cách mạng tháng tám 1945
-
 Dạng bài tập đoạn mạch song song
Dạng bài tập đoạn mạch song song
-
 CUỘC CÁCH MẠNG KHOA HỌC KĨ THUẬT LẦN THỨ HAI
CUỘC CÁCH MẠNG KHOA HỌC KĨ THUẬT LẦN THỨ HAI
-
 TRỢ TỪ – THÁN TỪ – TÌNH THÁI TỪ
TRỢ TỪ – THÁN TỪ – TÌNH THÁI TỪ
Thống kê
- Đang truy cập79
- Hôm nay24,645
- Tháng hiện tại744,771
- Tổng lượt truy cập18,832,955
Tài liệu mới
- chuyên đề Phương trình... - 18/04/2022
- Phương trình chứa ấn ở... - 28/02/2020
- Các dạng bài tập phương... - 28/02/2020
- Giáo án dạy thêm toán 6 - 27/02/2020
- Chuyên đề bồi dưỡng học... - 27/02/2020
