PHƯƠNG TRÌNH - HỆ PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH
A.KIẾN THỨC CƠ BẢN
1.Phương trình bậc nhất một ẩn
1.Phương trình bậc nhất một ẩn

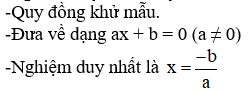
2.Phương trình chứa ẩn ở mẫu
-Tìm ĐKXĐ của phương trình.
-Quy đồng và khử mẫu.
-Giải phương trình vừa tìm được.
-So sánh giá trị vừa tìm được với ĐKXĐ rồi kết luận.
3.Phương trình tích
Để giái phương trình tích ta chỉ cần giải các phương trình thành phần của nó. Chẳng hạn: Với phương trình A(x).B(x).C(x) = 0
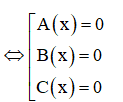
4.Phương trình có chứa hệ số chữ (Giải và biện luận phương trình)
Dạng phương trình này sau khi biến đổi cũng có dạng ax + b = 0. Song giá trị cụ thể của a, b ta không biết nên cần đặt điều kiện để xác định số nghiệm của phương trình.

6.Hệ phương trình bậc nhất
Cách giải chủ yếu dựa vào hai phương pháp cộng đại số và thế. Chú ý phương pháp đặt ẩn phụ trong một số trường hợp xuất hiện các biểu thức giống nhau ở cả hai phương trình.
7.Bất phương trình bậc nhất
Với bất phương trình bậc nhất thì việc biến đổi tương tự như với phương trình bậc nhất. Tuy nhiên cần chú ý khi nhân và cả hai vế với cùng một số âm thì phải đổi chiều bất phương trình.
B.MỘT SỐ VÍ DỤ
VD1.Giải các phương trình sau
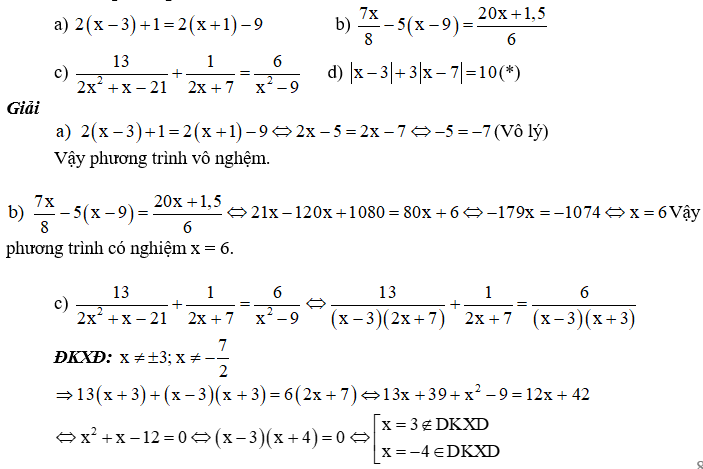

VD2.Giải và biện luận phương trình sau

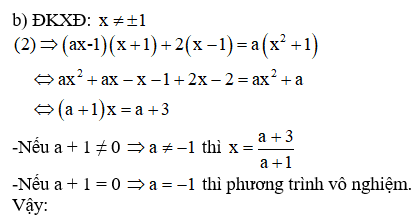

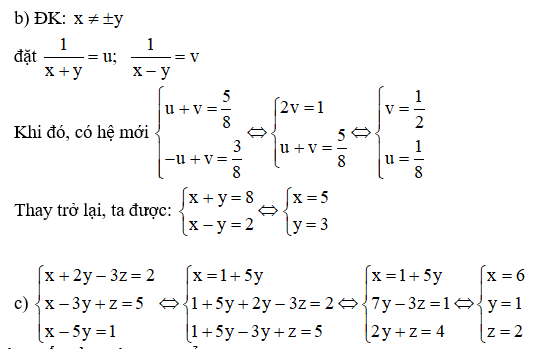
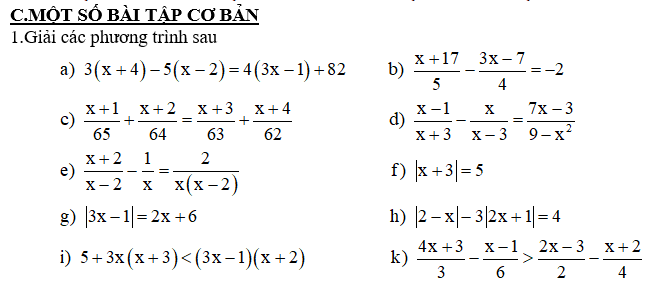

Ý kiến bạn đọc
Bạn cần đăng nhập với tư cách là Thành viên chính thức để có thể bình luận
Những tin mới hơn
Những tin cũ hơn
global video
-
-
 Hướng dẫn giải bài tập về vận...
hướng dẫn ôn tập và giải các bài tập về
Hướng dẫn giải bài tập về vận...
hướng dẫn ôn tập và giải các bài tập về
-
 Hướng dẫn giải bài tập về công...
hướng dẫn ôn tập và giải các bài tập về công cơ học
Hướng dẫn giải bài tập về công...
hướng dẫn ôn tập và giải các bài tập về công cơ học
-
 Hướng dẫn giải bài tập về lực...
Hướng dẫn giải bài tập về
Hướng dẫn giải bài tập về lực...
Hướng dẫn giải bài tập về
Thăm dò ý kiến
Tin xem nhiều
-
 Bài tập về thấu kính hội tụ
Bài tập về thấu kính hội tụ
-
 DẠNG TOÁN HỖN HỢP TRONG HÓA HỌC
DẠNG TOÁN HỖN HỢP TRONG HÓA HỌC
-
 ĐỀ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 MÔN GDCD
ĐỀ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 MÔN GDCD
-
 ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 MÔN NGỮ VĂN
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 MÔN NGỮ VĂN
-
 Bài tập về thấu kính phân kỳ
Bài tập về thấu kính phân kỳ
-
 Dạng bài tập về Đoạn mạch nối tiếp
Dạng bài tập về Đoạn mạch nối tiếp
-
 Cách mạng tháng tám 1945: Thời cơ, diễn biến, ý nghĩa lịch sử và bài học kinh nghiệm của cách mạng tháng tám 1945
Cách mạng tháng tám 1945: Thời cơ, diễn biến, ý nghĩa lịch sử và bài học kinh nghiệm của cách mạng tháng tám 1945
-
 Dạng bài tập đoạn mạch song song
Dạng bài tập đoạn mạch song song
-
 CUỘC CÁCH MẠNG KHOA HỌC KĨ THUẬT LẦN THỨ HAI
CUỘC CÁCH MẠNG KHOA HỌC KĨ THUẬT LẦN THỨ HAI
-
 TRỢ TỪ – THÁN TỪ – TÌNH THÁI TỪ
TRỢ TỪ – THÁN TỪ – TÌNH THÁI TỪ
Thống kê
- Đang truy cập118
- Hôm nay11,482
- Tháng hiện tại731,396
- Tổng lượt truy cập18,819,580
Tài liệu mới
- chuyên đề Phương trình... - 18/04/2022
- Phương trình chứa ấn ở... - 28/02/2020
- Các dạng bài tập phương... - 28/02/2020
- Giáo án dạy thêm toán 6 - 27/02/2020
- Chuyên đề bồi dưỡng học... - 27/02/2020
