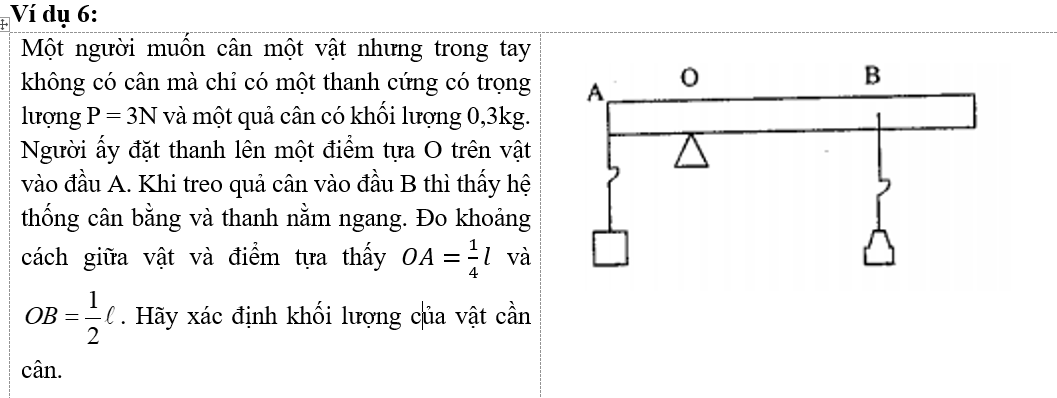
CÁC BÀI TOÁN LIÊN QUAN VỀ ĐÒN BẨY
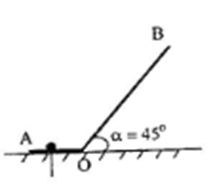
Ví dụ 1: Người ta dùng một xà beng có dạng như hình vẽ để nhổ một cây đinh cắm sâu vào gỗ.
a) Khi tác dụng một lực F = 100N vuông góc với OB tại đầu B ta sẽ nhổ được đinh. Tính lực giữ của gỗ vào đinh . Biết OB = 10.OA và \alpha = {45}^o
b) Nếu lực tác dụng vào đầu B vuông góc với tấm gỗ thì phải tác dụng một lực có độ lớn bằng bao nhiêu mới nhổ được đinh.
a) Khi tác dụng một lực F = 100N vuông góc với OB tại đầu B ta sẽ nhổ được đinh. Tính lực giữ của gỗ vào đinh . Biết OB = 10.OA và \alpha = {45}^o
b) Nếu lực tác dụng vào đầu B vuông góc với tấm gỗ thì phải tác dụng một lực có độ lớn bằng bao nhiêu mới nhổ được đinh.

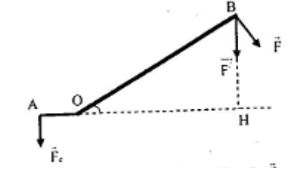
Hướng dẫn:
+ Điểm tựa tại O. Gọi Fc
+ Vì Fc

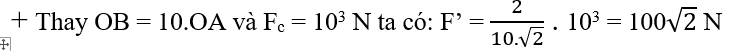
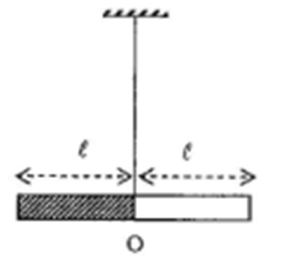
Ví dụ 2: Hai bản kim loại đồng chất tiết diện đều có cùng chiều dài l = 20cm và cùng tiết diện nhưng có trọng lượng riêng khác nhau d1 = 1,25.d2. Hai bản được hàn dính lại ở một đầu O và được treo bằng sợi dây. Để thanh nằm ngang người ta thực hiện hai biện pháp sau:
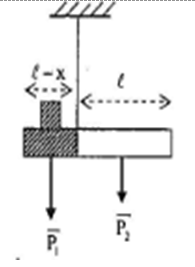
a) Cắt một phần của thanh thứ nhất và đem đặt lên chính giữa của phần còn lại. Tìm chiều dài phần bị cắt.
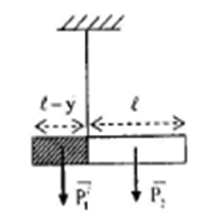
b) Cắt bỏ một phần của bản thứ nhất. Tìm phần bị cắt đi.
Hướng dẫn:
a) Vì cắt một phần của bản thứ nhất và lại đặt lên chính giữa của phần còn lại nên lực tác dụng không thay đổi, cánh tay đòn của lực này thì thay đổi.
+ Gọi x là chiều dài phần bị cắt. Do được đặt lên chính giữa của phần còn lại nên trọng lượng của bản thứ nhất ko thay đổi. Điểm đặt của trọng lực P1

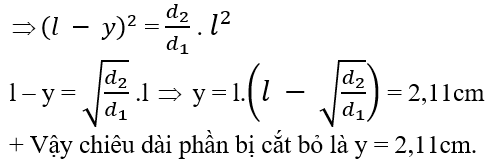
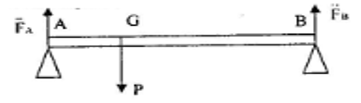
Ví dụ 3: Một chiếc xà không đồng chấy dài l = 8m. Khối lượng 120 kg được tì đầu A, B lên hai bức tường. Trọng tâm của xà cách đầu A một khoảng GA = 3m. Hãy xác định lực đỡ của tường lên các đầu xà
Hướng dẫn:
+ Trọng lượng của xà bằng: P = 10.120 = 1200N
+ Trọng tâm của xà tập trung tại trọng tâm G của xà
+ Xà có hai điểm tựa (hai giá đỡ), xà chịu tác dụng của 3 lực FA
* Để tính FA ta coi xà là một đòn bẩy có điểm tựa tại B.
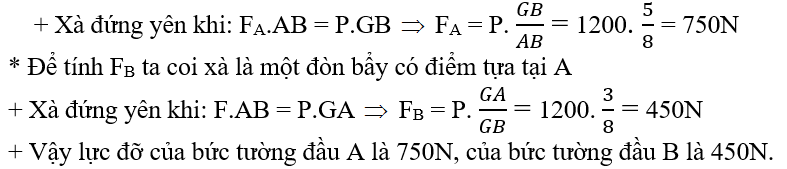
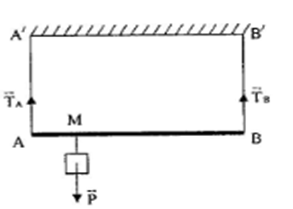
Ví dụ 4: Một cái sào được treo theo phương nằm ngang bằng hai sợi dây AA’ và BB’. Tại điểm M người ta treo một vật nặng có khối lượng 70kg. Tính lực căng của các sơi dây AA’ và BB’. Cho biết: AB = 1,4m; AM = 0,2m.
Hướng dẫn:
+ Trọng lượng của vật nặng là: P = 10.70 = 700N
+ Gọi lực căng của các sợi đây AA’ và BB’ lần lượt là TA và TB.
+ Cái sào chịu tác dụng của 3 lực TA, TB và P.
* Đề tính TA coi sào như một đòn bẩy có điểm tựa tại B.
+ Để sào nằm ngang ta có: TA.AB = P.MB

Ví dụ 5: Một chiếc xà đồng chất tiết diện đều. Khối lượng 20 kg, chiều dài 3 m. Tì hai đầu lên hai bức tường. Một người có khối lượng 75 kg đứng cách đầu xà 2m. Xác định xem mỗi bức tường chịu tác dụng một lực bằng bao nhiêu?
Hướng dẫn:
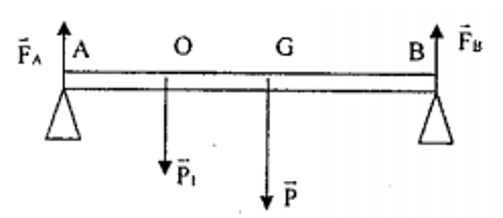
- Các lực tác dụng lên xà là:
- Lực đỡ FA ,FB
- Trọng lượng của xà: P = 10.20 = 200 (N)
- Trọng lượng của người P1 = 10.75 = 750 (N)Vì xà đồng chất tiết diện đều nên trọng tâm của xà sẽ ở chính giữa xà
- => GA = GB = l,5 m
- Giả sử người đứng ở O cách A là OA = 2m
- Áp dụng quy tắc cân bằng của đòn bây khi có nhiều lực tác dụng ta có:

Hướng dẫn:
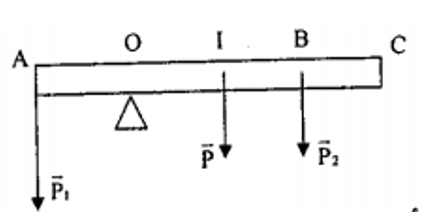
- Các lực tác dụng lên thanh AC
- Trọng lượng P1, P2; của các vật treo tại A và B

Hướng dẫn:
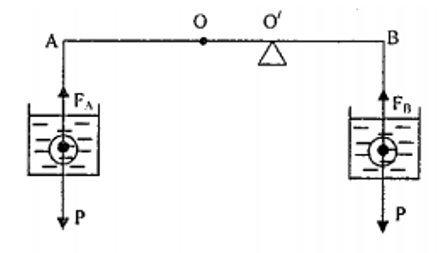
- Vì trọng lượng hai quả cầu cân bằng nhau nên lúc đâu điểm tựa O ở chính giữa đòn
- Khi nhúng A, B vào nước O’A = 48 cm, O’B = 36 cm

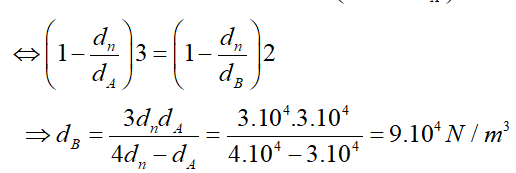
 = 25 cm. Nhúng quả cầu ở đầu B vào nước thanh AB mất thăng bằng. Để thanh thăng bằng trở lại ta phải dời điểm treo O về phía nào? Một đoạn bao nhiêu? Cho khối lượng riêng của nhôm và nước lần lượt là: D1 = 2,7 g/cm3; D2 = 1 g/cm3
= 25 cm. Nhúng quả cầu ở đầu B vào nước thanh AB mất thăng bằng. Để thanh thăng bằng trở lại ta phải dời điểm treo O về phía nào? Một đoạn bao nhiêu? Cho khối lượng riêng của nhôm và nước lần lượt là: D1 = 2,7 g/cm3; D2 = 1 g/cm3
Hướng dẫn:
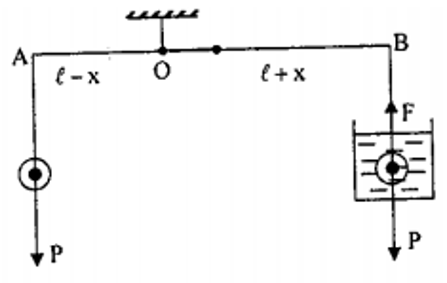
Khi quả cầu treo ở B được nhúng vào nước, ngoài trọng lượng P nó còn chịu tác dụng của lực đẩy Acsimet nên lực tổng hợp giảm xuống. Do đó cần phải dịch chuyển điểm treo về phía A một đoạn x để cho cánh tay đòn của quả cầu B tăng lên.

Ví dụ 9: Một thanh AB có trọng lượng P = 100 N
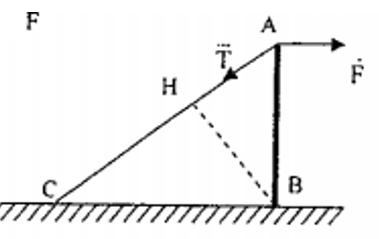
a) Đầu tiên thanh được đặt thẳng đứng chịu tác dụng của một lực F = 200 N theo phương ngang. Tìm lực căng của sợi dây AC. Biết AB = BC.
b) Sau đó người ta đặt thanh nằm ngang gắn vào tường nhờ bản lề tại B. Tìm lực căng của dây AC lúc này. Biết AB = BC.
Hướng dẫn:
a) Do lực F đi qua điểm quay B nên không ảnh hưởng đến sự quay.
đi qua điểm quay B nên không ảnh hưởng đến sự quay.
+ Thanh AB chịu tác dụng của lực và
và 
+ Lực có cánh tay đòn là AB
có cánh tay đòn là AB
+ Lực có cánh tay đòn là BH
có cánh tay đòn là BH
+ Đề thanh cần băng ta có: F.AB =T.BH
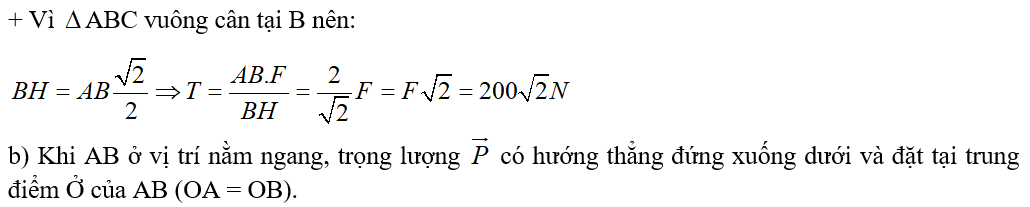
+ Thanh AB có điểm quay tại B
+ Cánh tay đòn của là OB
là OB
+ Cánh tay đòn của là BH
là BH
+ Vị ABC vuông cân tại B nên:
ABC vuông cân tại B nên:

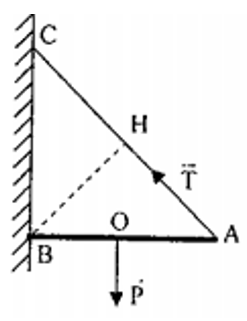
Ví dụ 10: Một khối trụ lục giác đều, được đặt trên mặt sàn nằm ngang. Một lực F tác dụng theo phương ngang đặt vào đỉnh C như hình vẽ. Trụ có thể quay quanh A.
tác dụng theo phương ngang đặt vào đỉnh C như hình vẽ. Trụ có thể quay quanh A.
a) Xác định độ lớn của lực để khối trụ còn cân bằng. Biết trọng lượng của khối trụ là P = 30 N.
để khối trụ còn cân bằng. Biết trọng lượng của khối trụ là P = 30 N.
b) Lực theo hướng nào thì độ lớn lực bé nhất sao cho khối trụ vẫn nằm cân bằng. Tính Fmin khi đó (lực F vẫn đặt tại C).
theo hướng nào thì độ lớn lực bé nhất sao cho khối trụ vẫn nằm cân bằng. Tính Fmin khi đó (lực F vẫn đặt tại C).
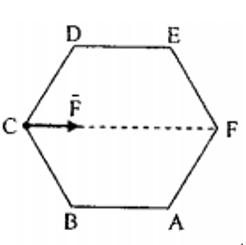

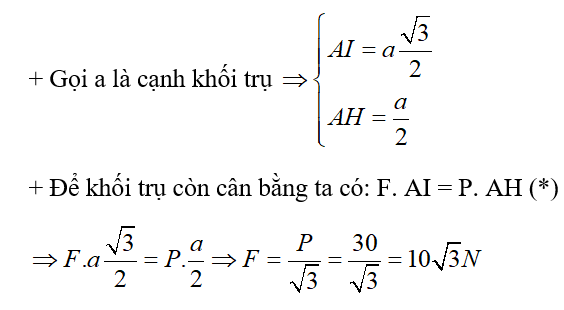

Ta có x = AI’ = AC.cosa và AI’ lớn nhất khi cosa = max = l => a = 0
Lúc đó AI’ = AC => l’ trùng vào C.
Vậy khi trùng vào CD thì Fmin
trùng vào CD thì Fmin
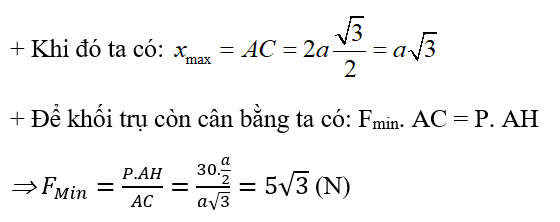
Ví dụ 11: Cho một thước thẳng AB đồng chất tiết diện đều, có độ dài l = 24 cm trọng lượng P = 4 N. Đầu A treo một vật có trọng lượng P1 = 2N. Thước đặt lên một giá đỡ nằm ngang CD = 4 cm. Xác định giá trị lớn nhất và nhỏ nhất của khoảng cách BD để cho thước nằm cân bằng trên giá đỡ.
Hướng dẫn:
+ Xét trạng thái cân bằng của thước quanh trục đi qua mép D của giá đỡ ứng với giá trị nhỏ nhất của AD. Lúc đó thước chia làm hai phần: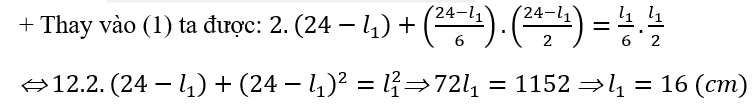
+ Giá trị lớn nhất của BD là l1 = 16 (cm). Lúc đó điểm D trùng với điểm E trên thước BE = BD = 16 cm
+ Nếu ta di chuyển thước từ phải sang trái sao cho điểm E trên thước còn nằm trên giá CD thì thước vẫn cân bằng cho tới khi E trùng với C thì đến giới hạn cân bằng E lệch ra ngoài CD về phía trái thì thước sẽ quay quanh trục C sang trái.
+ Vậy giá trị nhỏ nhất của BD khi C trùng đến E là BE = BC
+ Mà BC = BD + DC => BD = BC – DC = 16 – 4 = 12 (cm)
Ví dụ 12: Một thanh thẳng đồng chất tiết diện đều có trọng lượng P = 100 N, chiều dài AB = 100 cm, được đặt cân bằng trên hai giá đỡ ở A và C. Điểm C cách tâm O của thước một đoạn OC = x
a) Tìm công thức tính áp lực của thước lên giá đỡ ở C theo x.
b) Tìm vị trí của C để áp lực ở đó có giá trị cực đại, cực tiểu.
Hướng dẫn:
a) Trọng lượng P của thanh đặt tại trọng tâm O là trung điểm của thanh tác dụng lên hai giá đỡ A và B hai áp lực P1 và P2.
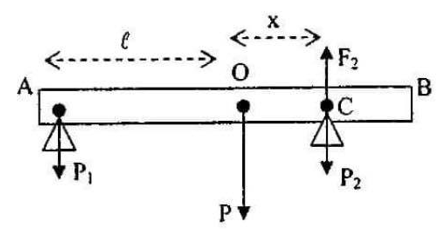
+ Áp lực P2 có độ lớn bằng với phản lực F2 tại C. Để tính P2 ta sẽ tìm F2


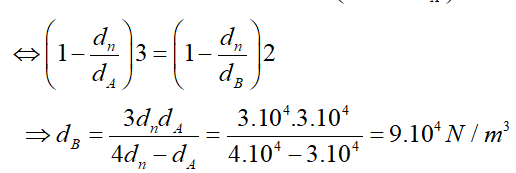
- Vậy trọng lượng riêng của quả cầu B là: dB = 9.104 N/m3
Hướng dẫn:
Khi quả cầu treo ở B được nhúng vào nước, ngoài trọng lượng P nó còn chịu tác dụng của lực đẩy Acsimet nên lực tổng hợp giảm xuống. Do đó cần phải dịch chuyển điểm treo về phía A một đoạn x để cho cánh tay đòn của quả cầu B tăng lên.


Ví dụ 9: Một thanh AB có trọng lượng P = 100 N
a) Đầu tiên thanh được đặt thẳng đứng chịu tác dụng của một lực F = 200 N theo phương ngang. Tìm lực căng của sợi dây AC. Biết AB = BC.
b) Sau đó người ta đặt thanh nằm ngang gắn vào tường nhờ bản lề tại B. Tìm lực căng của dây AC lúc này. Biết AB = BC.

Hướng dẫn:
a) Do lực F
 đi qua điểm quay B nên không ảnh hưởng đến sự quay.
đi qua điểm quay B nên không ảnh hưởng đến sự quay.+ Thanh AB chịu tác dụng của lực
+ Lực
+ Lực
+ Đề thanh cần băng ta có: F.AB =T.BH
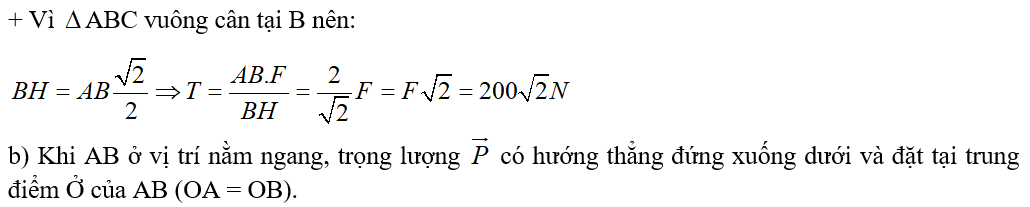
+ Thanh AB có điểm quay tại B
+ Cánh tay đòn của
+ Cánh tay đòn của
+ Vị


Ví dụ 10: Một khối trụ lục giác đều, được đặt trên mặt sàn nằm ngang. Một lực F
 tác dụng theo phương ngang đặt vào đỉnh C như hình vẽ. Trụ có thể quay quanh A.
tác dụng theo phương ngang đặt vào đỉnh C như hình vẽ. Trụ có thể quay quanh A.a) Xác định độ lớn của lực
b) Lực


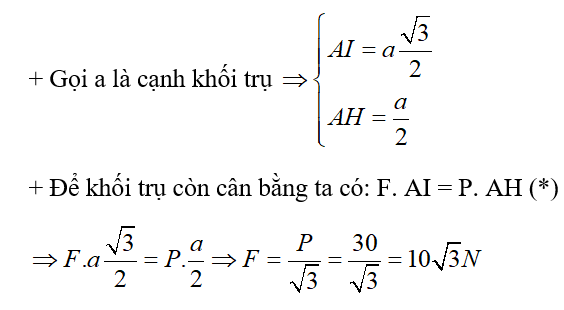

Ta có x = AI’ = AC.cosa và AI’ lớn nhất khi cosa = max = l => a = 0
Lúc đó AI’ = AC => l’ trùng vào C.
Vậy khi
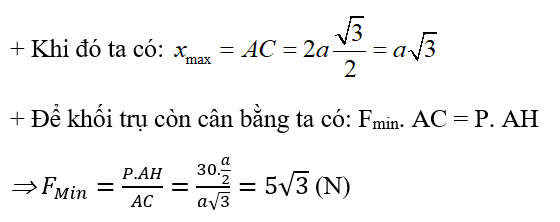
Ví dụ 11: Cho một thước thẳng AB đồng chất tiết diện đều, có độ dài l = 24 cm trọng lượng P = 4 N. Đầu A treo một vật có trọng lượng P1 = 2N. Thước đặt lên một giá đỡ nằm ngang CD = 4 cm. Xác định giá trị lớn nhất và nhỏ nhất của khoảng cách BD để cho thước nằm cân bằng trên giá đỡ.
Hướng dẫn:
+ Xét trạng thái cân bằng của thước quanh trục đi qua mép D của giá đỡ ứng với giá trị nhỏ nhất của AD. Lúc đó thước chia làm hai phần:
- Phần BD có trọng lượng P3 đặt ở G1 là trung điểm của DB
- Phần AD có trọng lượng P2 đặt ở G2 là trung điểm của AD
- Mép D ở điểm E trên thước.
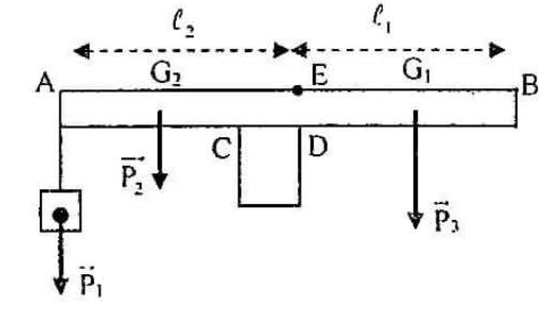

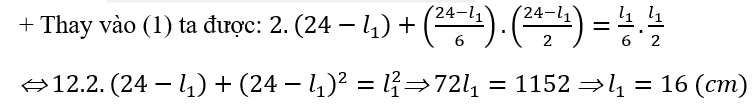
+ Giá trị lớn nhất của BD là l1 = 16 (cm). Lúc đó điểm D trùng với điểm E trên thước BE = BD = 16 cm
+ Nếu ta di chuyển thước từ phải sang trái sao cho điểm E trên thước còn nằm trên giá CD thì thước vẫn cân bằng cho tới khi E trùng với C thì đến giới hạn cân bằng E lệch ra ngoài CD về phía trái thì thước sẽ quay quanh trục C sang trái.
+ Vậy giá trị nhỏ nhất của BD khi C trùng đến E là BE = BC
+ Mà BC = BD + DC => BD = BC – DC = 16 – 4 = 12 (cm)
Ví dụ 12: Một thanh thẳng đồng chất tiết diện đều có trọng lượng P = 100 N, chiều dài AB = 100 cm, được đặt cân bằng trên hai giá đỡ ở A và C. Điểm C cách tâm O của thước một đoạn OC = x
a) Tìm công thức tính áp lực của thước lên giá đỡ ở C theo x.
b) Tìm vị trí của C để áp lực ở đó có giá trị cực đại, cực tiểu.
Hướng dẫn:
a) Trọng lượng P của thanh đặt tại trọng tâm O là trung điểm của thanh tác dụng lên hai giá đỡ A và B hai áp lực P1 và P2.

+ Áp lực P2 có độ lớn bằng với phản lực F2 tại C. Để tính P2 ta sẽ tìm F2
- Để tìm phản lực F2 ta chọn điểm tựa tại A
- Trọng lực P đặt tại trọng tâm O (chính giữa thanh AB)
- Phản lực F2 đặt tại C
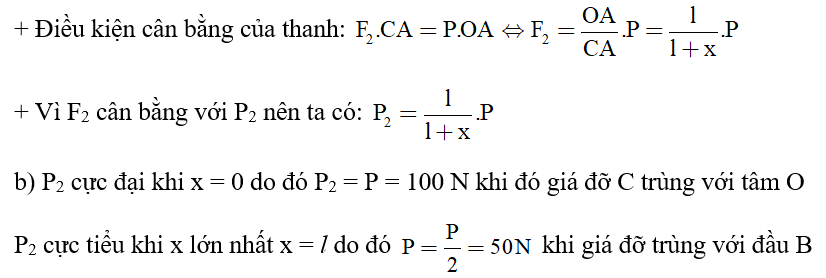
Ý kiến bạn đọc
Bạn cần đăng nhập với tư cách là Thành viên chính thức để có thể bình luận
Những tin mới hơn
Những tin cũ hơn
global video
-
-
 Hướng dẫn giải bài tập về vận...
hướng dẫn ôn tập và giải các bài tập về
Hướng dẫn giải bài tập về vận...
hướng dẫn ôn tập và giải các bài tập về
-
 Hướng dẫn giải bài tập về công...
hướng dẫn ôn tập và giải các bài tập về công cơ học
Hướng dẫn giải bài tập về công...
hướng dẫn ôn tập và giải các bài tập về công cơ học
-
 Hướng dẫn giải bài tập về lực...
Hướng dẫn giải bài tập về
Hướng dẫn giải bài tập về lực...
Hướng dẫn giải bài tập về
Thăm dò ý kiến
Tin xem nhiều
-
 Bài tập về thấu kính hội tụ
Bài tập về thấu kính hội tụ
-
 DẠNG TOÁN HỖN HỢP TRONG HÓA HỌC
DẠNG TOÁN HỖN HỢP TRONG HÓA HỌC
-
 ĐỀ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 MÔN GDCD
ĐỀ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 9 MÔN GDCD
-
 ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 MÔN NGỮ VĂN
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 MÔN NGỮ VĂN
-
 Bài tập về thấu kính phân kỳ
Bài tập về thấu kính phân kỳ
-
 Dạng bài tập về Đoạn mạch nối tiếp
Dạng bài tập về Đoạn mạch nối tiếp
-
 Cách mạng tháng tám 1945: Thời cơ, diễn biến, ý nghĩa lịch sử và bài học kinh nghiệm của cách mạng tháng tám 1945
Cách mạng tháng tám 1945: Thời cơ, diễn biến, ý nghĩa lịch sử và bài học kinh nghiệm của cách mạng tháng tám 1945
-
 Dạng bài tập đoạn mạch song song
Dạng bài tập đoạn mạch song song
-
 CUỘC CÁCH MẠNG KHOA HỌC KĨ THUẬT LẦN THỨ HAI
CUỘC CÁCH MẠNG KHOA HỌC KĨ THUẬT LẦN THỨ HAI
-
 TRỢ TỪ – THÁN TỪ – TÌNH THÁI TỪ
TRỢ TỪ – THÁN TỪ – TÌNH THÁI TỪ
Thống kê
- Đang truy cập75
- Hôm nay19,979
- Tháng hiện tại729,578
- Tổng lượt truy cập18,817,762
Tài liệu mới
- chuyên đề Phương trình... - 18/04/2022
- Phương trình chứa ấn ở... - 28/02/2020
- Các dạng bài tập phương... - 28/02/2020
- Giáo án dạy thêm toán 6 - 27/02/2020
- Chuyên đề bồi dưỡng học... - 27/02/2020
