HÌNH CHỮ NHẬT

Thứ năm - 08/10/2020 10:31

Bài 1:
Cho tứ giác ABCD. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng MNPQ là hình bình hành.
Tứ giác ABCD cần điều kiện gì thì MNPQ là hình chữ nhật.

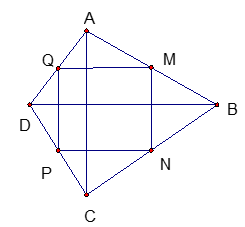
Trong tam giác ABD có QM là đường trung bình nên QM // BD và QM = 1/2.BD
Tương tự trong tam giác BCD có PN là đường trung bình nên PN // BD và
PN = 1/2.BD
Vậy PN // QM và PN // QM
Hay MNPQ là hình bình hành.
Để MNPQ là hình chữ nhật thì AC và BD vuông góc với nhau vì khi đó hình bình hành có 1 góc vuông.
Bài 2:
Cho tứ giác ABCD. Gọi O là giao điểm của 2 đường chéo ( không vuông góc),I và K lần lượt là trung điểm của BC và CD. Gọi M và N theo thứ tự là điểm đối xứng của điểm O qua tâm I và K.
a) C/m rằng tứ giác BMND là hình bình hành.
b) Với điều kiện nào của hai đường chéo AC và BD thì tứ giác BMND là hình chữ nhật.
c) Chứng minh 3 điểm M,C,N thẳng hàng.
- GV yêu cầu HS lên bảng vẽ hình, ghi giả thiết , kết luận.

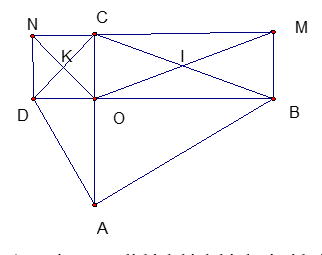
a/ Ta có OCND là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường. Do đó OC // ND và OC = ND.
Tương tự ta có OCBM là hình bình hành nên OC // MB và OC = MB
Vậy MB // DN và MB = DN
Hay BMND là hình bình hành.
b/ Để BMND là hình chữ nhật thì
COB = 90⁰ hay CA và BD vuông góc.
c/ Ta có OCND là hình bình hành nên
NC // DO, Tứ giác BMND là hình bình hành nên MN // BD .
Mà qua N chỉ có một đường thẳng song song với BD do đó M, N, C thẳng hàng.

Bài 3:
Cho tam giác ABC, các trung tuyến BM và CN cắt nhau ở G. Gọi P là điểm đối xứng của điểm M qua B. Gọi Q là điểm đối xứng của điểm N qua G.
a/ Tứ giác MNPQ là hình gì? Vì sao ?
b/ Nếu ABC cân ở A thì tứ giác MNPQ là hình gì ? Vì sao?

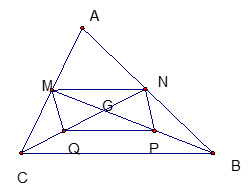
a/ Ta có MG = GP = 1/3.BM
GQ = GN = 1/3.CN.
Vậy MNPQ là hình bình hành.
b/ Tam giác ABC cân tại A nên BM = NC.
Khi đó QN = MP = 2/3 BM = 2/3 CN.
Vậy MNPQ là hình chữ nhật.